leetcode刷题记录——二叉树

104. 二叉树的最大深度 Easy

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

104.1

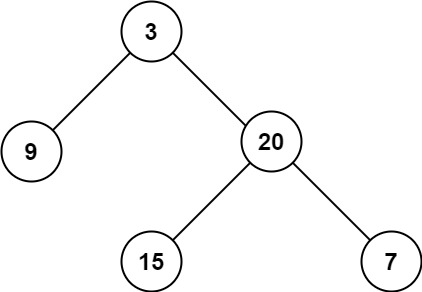
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

树中节点的数量在 [0, 104] 区间内。

-100 <= Node.val <= 100

思路

这题基本上没啥好说的🤣，就是两个maxDepth最后加个1

代码

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

时间复杂度

时间复杂度O(n)，空间复杂度O(h)，执行时间43ms，消耗内存17.7MB

100 相同的树 Easy

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

100.1

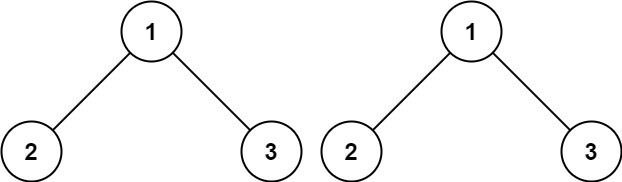
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

100.2

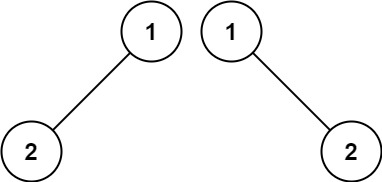
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

100.3

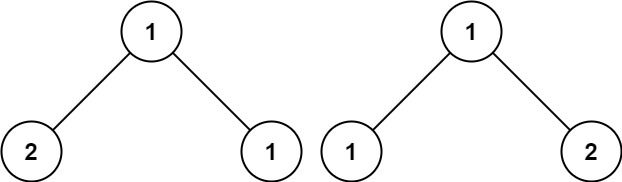
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内

-104 <= Node.val <= 104

思路

这里也一样，没什么好说的。我这里条件写的有点复杂，我看好一点的两个判断语句搞定，有一个一个判断语句搞定。后面直接用isSameTree就搞定（简单题你还指望我干啥，造火箭吗）

代码

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if not p and not q:
            return True
        if not p or not q:
            return False
        if p.val != q.val:
            return False
        return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

时间复杂度

时间复杂度O(n)，空间复杂度O(h)，执行时间48ms，消耗内存16，2MB

226 翻转二叉树 Easy

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

226.1

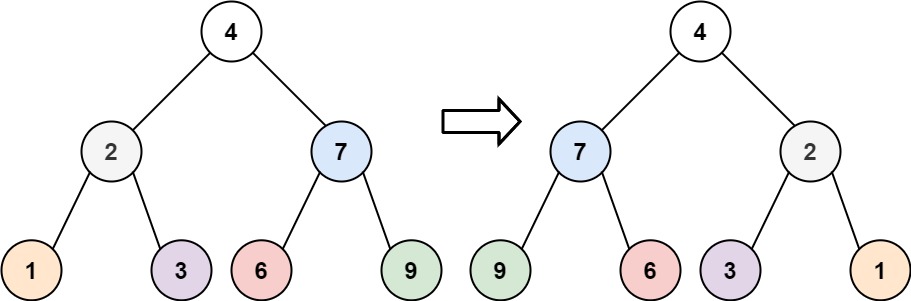
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

226.2

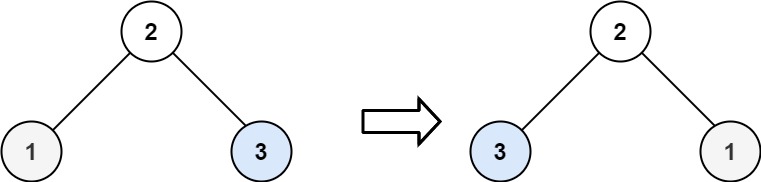
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内

-100 <= Node.val <= 100

思路

思路上没啥难的，但是！那个梗真的好好笑，我之前真的不知道这个梗。翻评论看到半天没反应过来咋回事，一搜才知道。

代码

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root:
            return None
        root.left, root.right = root.right, root.left
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间27ms，消耗内存16.2MB

101 对称二叉树 Easy

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

101.1

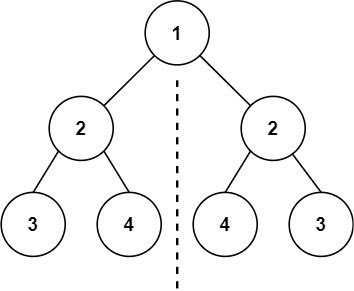
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

101.2

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内

-100 <= Node.val <= 100

思路

递归判断，如果左子树和右子树对称，那么左子树的左子树和右子树的右子树都是对称的，左子树的右子树和右子树的左子树都是对称的。

代码

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        def isMirror(left, right):
            if not left and not right:
                return True
            if not left or not right or left.val != right.val:
                return False
            return isMirror(left.left, right.right) and isMirror(left.right, right.left)
        return isMirror(root.left, root.right)

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间48ms，消耗内存16.4MB

105 从前序与中序遍历序列构造二叉树 Medium

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

105.1

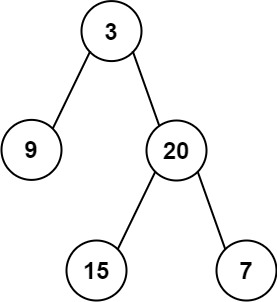
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000

inorder.length == preorder.length

-3000 <= preorder[i], inorder[i] <= 3000

preorder 和 inorder 均 无重复 元素

inorder 均出现在 preorder

preorder 保证 为二叉树的前序遍历序列

inorder 保证 为二叉树的中序遍历序列

思路

1. 根据前序遍历可以得到根节点就是 TreeNode[0] ，再根据中序遍历可以得到根节点的左右子树，然后递归，继续求就可以了
2. 注意边界条件，如果前序遍历为空或中序遍历为空，那么返回空

代码

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder or not inorder:
            return None
        root = TreeNode(preorder[0])
        mid = inorder.index(preorder[0])
        root.left = self.buildTree(preorder[1 : mid + 1], inorder[: mid])
        root.right = self.buildTree(preorder[mid + 1 :], inorder[mid + 1 :])
        return root

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间149ms，消耗内存86.4MB

106 从中序与后序遍历序列构造二叉树 Medium

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

106.1

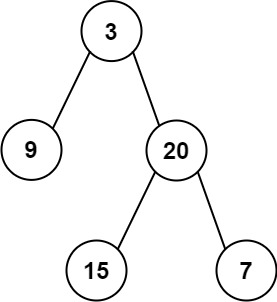
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000

postorder.length == inorder.length

-3000 <= inorder[i], postorder[i] <= 3000

inorder 和 postorder 都由 不同 的值组成

postorder 中每一个值都在 inorder 中

inorder 保证是树的中序遍历

postorder 保证是树的后序遍历

思路

和105一样，通过后序遍历得到根节点（最后一个就是），然后通过中序遍历得到根节点的左右子树，然后递归，继续求就可以了

代码

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        if not inorder or not postorder:
            return None
        root = TreeNode(postorder[-1])
        mid = inorder.index(postorder[-1])
        root.left = self.buildTree(inorder[: mid], postorder[: mid])
        root.right = self.buildTree(inorder[mid + 1 : ], postorder[mid : -1])
        return root

时间复杂度

时间复杂度O(n)，空间复杂度O(n)执行时间143ms，消耗内存86.5MB

117 填充每个节点的下一个右侧节点指针ⅡMedium

给定一个二叉树：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

117.1

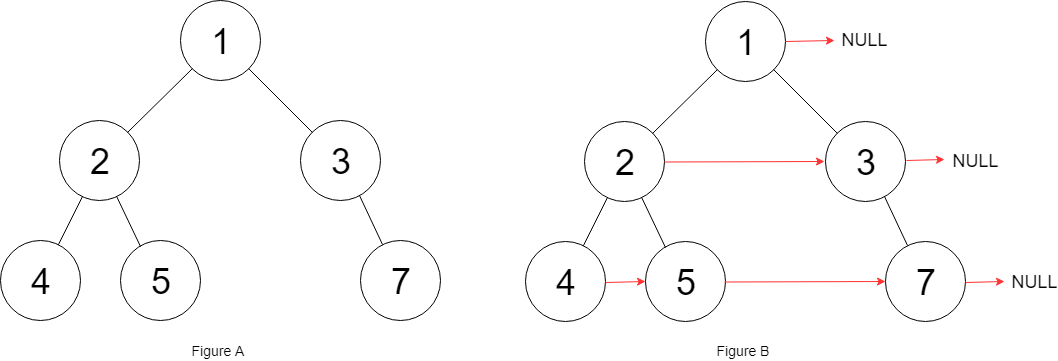
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

示例 2：

输入：root = []
输出：[]

提示：

树中的节点数在范围 [0, 6000] 内

-100 <= Node.val <= 100

思路

这里直接考虑DFS或BFS。

我采用的是BFS，通过一个列表来存储最终结果，通过另一个列表来存储每一层的节点。

有当前节点的左右节点就加入到队列中，然后用一个循环进行遍历将每一次节点连接起来（仅本层）

代码

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return root
        queue = [root]
        while queue:
            next_queue = []
            for node in queue:
                if node.left:
                    next_queue.append(node.left)
                if node.right:
                    next_queue.append(node.right)
            for i in range(len(queue) - 1):
                queue[i].next = queue[i + 1]
            queue = next_queue
        return root

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间46ms，消耗内存17.4MB

114 二叉树展开为链表 Medium

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。

展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

114.1

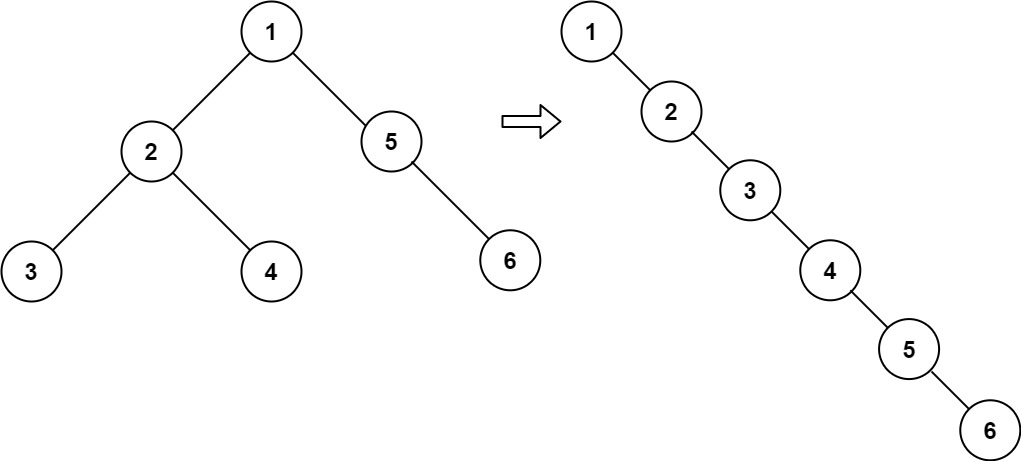
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内

-100 <= Node.val <= 100

思路

这里需要涉及到一个函数 flatten，该函数会自动将树拉直，所以我们分别让左右子树拉直然后右子树接在左子树后面就可以了

代码

class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        if not root:
            return root
        self.flatten(root.left)
        self.flatten(root.right)
        
        left = root.left
        right = root.right
        
        root.left = None
        root.right = left
        
        p = root
        while p.right:
            p = p.right
        p.right = right
            
        return root

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间36ms，消耗内存16.7MB

112 路径之和 Easy

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

112.1

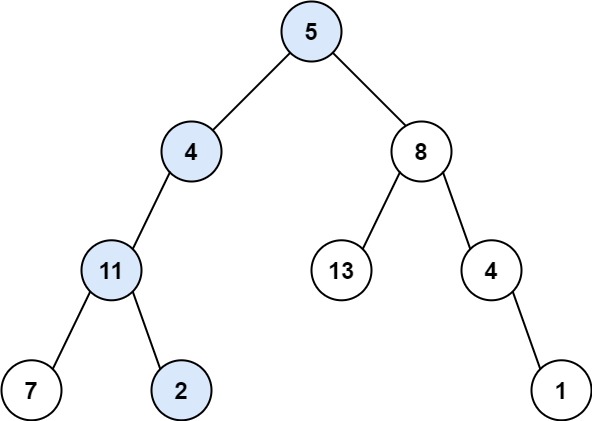
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

112.2

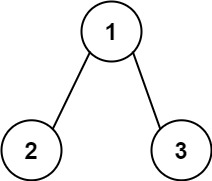
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内

-1000 <= Node.val <= 1000

-1000 <= targetSum <= 1000

思路

这题的核心在于使用一个函数hashPathSum，函数有两个参数（当前子树root，剩余目标sum），最终输出一个bool变量。

代码

class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        if not root:
            return False
        if not root.left and not root.right and root.val == targetSum:
            return True
        return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间41ms，消耗内存17.5MB

129 求根节点到叶子节点数字之和 Medium

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

129.1

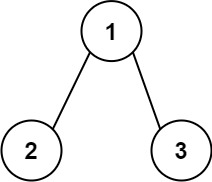
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

129.2

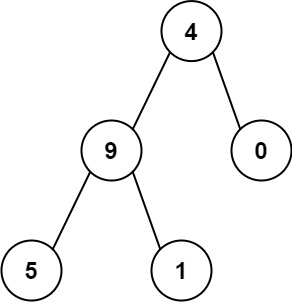
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

树中节点的数目在范围 [1, 1000] 内

0 <= Node.val <= 9

树的深度不超过 10

思路

用递归去解决，值就是原本的值*10加当前节点的值，处理方法还是很好理解的，然后分别对左右子树进行递归，搞定。

进入二叉树的条件是dfs(root, 0)

代码

class Solution:
    def sumNumbers(self, root: Optional[TreeNode]) -> int:
        def dfs(node, path):
            if node is None:
                return
            path = path * 10 + node.val
            if not node.left and not node.right:
                self.ans += path
            dfs(node.left, path)
            dfs(node.right, path)
                
        self.ans = 0
        dfs(root, 0)
        return self.ans

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间37ms，消耗内存16.4MB

124 二叉树中的最大路径和 Hard

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

124.1

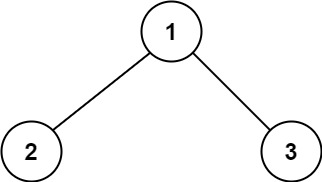
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

124.2

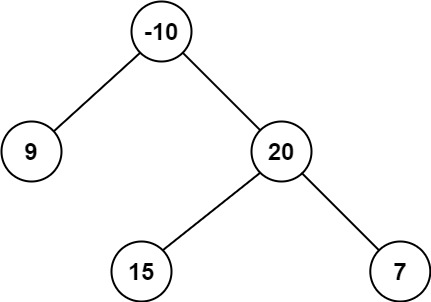
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]

-1000 <= Node.val <= 1000

思路

这里照样可以使用dfs的递归调用，不断更新最大值，最后返回最大值。

我的做法是直接使用类属性 self.ans 来记录最大值。这样作用域会更广，并且可以在其它类方法中使用。

不过相比于leetcode上大部分人所用的声明局部变量后通过 nonlocal 来转换为非局部变量，我的做法虽然可以在其它类中调用但是速度更慢一些。

代码

class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.ans = float('-inf')
        def dfs(node):
            if not node:
                return 0
            left = max(dfs(node.left), 0)
            right = max(dfs(node.right), 0)
            self.ans = max(self.ans, node.val + left + right)
            return node.val + max(left, right)
        dfs(root)
        return self.ans

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间80ms，消耗内存21.6MB

173 二叉搜索树递归器 Medium

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。

boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。

int next()将指针向右移动，然后返回指针处的数字。

注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：

173.1

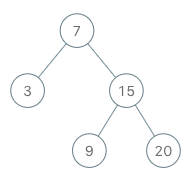
输入
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]

解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // 返回 3
bSTIterator.next();    // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 20
bSTIterator.hasNext(); // 返回 False

提示：

树中节点的数目在范围 [1, 105] 内

0 <= Node.val <= 106

最多调用 $10^5$ 次 hasNext 和 next 操作

思路

首先我最开始的写法发现pushAll已经不支持了，立马改写法

然后我们看正确代码，思路上还是使用一个双端队列来存结果。额外创建一个函数——中序遍历，用这个来将二叉树的节点进行遍历，然后我们按照题目给的意思去写 next 和 hashnext 函数。

这里需要注意一点题目中所说的当前节点的下一个节点有数返回True，这个直接转化为长度存在就返回True，这样可以避免看到题目第一反应用指针去做。

代码

错误版本

class BSTIterator:

    def __init__(self, root: Optional[TreeNode]):
        self.stack = []
        self.pushAll(root)

    def next(self) -> int:
        node = self.stack.pop()
        self.pushAll(node.right)
        return node.val

    def hasNext(self) -> bool:
        return len(self.stack) > 0

class BSTIterator:

    def __init__(self, root: Optional[TreeNode]):
        self.queue = collections.deque()
        self.inOrder(root)
    def inOrder(self, root):
        if not root: return 
        self.inOrder(root.left)
        self.queue.append(root.val)
        self.inOrder(root.right)

    def next(self) -> int:
        return self.queue.popleft()

    def hasNext(self) -> bool:
        return len(self.queue) > 0

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间74ms，消耗内存22.5MB

222 完全二叉树的节点数 Easy

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ $2^h$ 个节点。

示例 1：

222.1

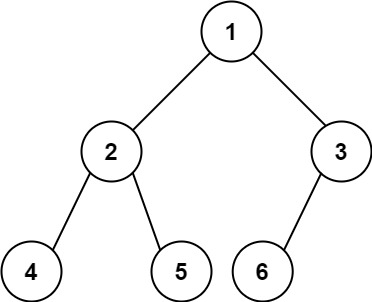
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

树中节点的数目范围是 [0, 5 * 104]

0 <= Node.val <= 5 * 104

题目数据保证输入的树是 完全二叉树

思路

直接调用countNode函数，记得分别对左右子树进行调用

代码

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间65ms，消耗内存22MB

236 二叉树的最近公共祖先 Medium

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

236.1

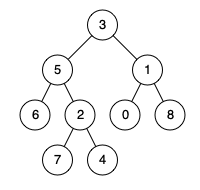
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

236.2

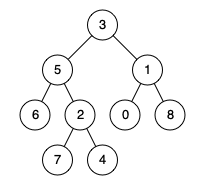
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 105] 内。

-109 <= Node.val <= 109

所有 Node.val 互不相同 。

p != q

p 和 q 均存在于给定的二叉树中。

思路

这里直接用lowestCommonAncestor函数，传入两个节点，返回公共祖先。

代码

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root or root == p or root == q: return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if left and right:
            return root
        return left if left else right

时间复杂度

时间复杂度O(n)，空间复杂度O(n)，执行时间47ms，消耗内存20.7MB