199 二叉树的右视图 Medium 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
199.1
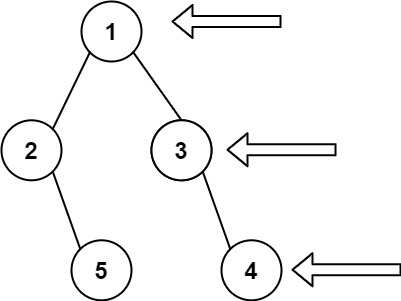
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:
输入: [1,null,3]
输出: [1,3]
示例 3:
输入: []
输出: []
提示:
二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100
思路 这里按照标题直接用DFS去遍历,保证我们首先处理的是右子树,这样遇到的第一个节点就会被压入。而当我们的有一层没有右子树的时候,就会将其左子树压入栈中。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution :def rightSideView (self, root: Optional [TreeNode] ) -> List [int ]:if not root:return []def dfs (node, depth ):if not node:return if depth == len (res):1 )1 )0 )return res
时间复杂度 时间复杂度O(n),空间复杂度O(n),执行时间41ms,消耗内存16.5MB
637 二叉树的层平均值 Easy 给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 $10^5$ 以内的答案可以被接受。
示例 1:
637.1
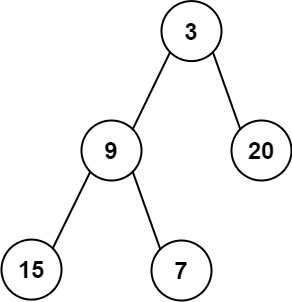
输入:root = [3,9,20,null,null,15,7]
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
示例 2:
637.2
输入:root = [3,9,20,15,7]
输出:[3.00000,14.50000,11.00000]
提示:
树中节点数量在 [1, 104] 范围内
-231 <= Node.val <= 231 - 1
思路 实际上就是每一层都需要被遍历到,当我们遇到有子节点的就把子节点存入 childNode 中然后再去走接下来的本层节点。后面把 childNode 导入我们最开始的全局变量 queue 中继续运行。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution :def averageOfLevels (self, root: Optional [TreeNode] ) -> List [float ]:if not root:return []while queue:sum = 0 len (queue)for node in queue:sum += node.valsum /cnt)for node in queue:if node.left:if node.right:return res
由于第一个代码中while循环又套了两个for循环,速度太慢,我就简化了一下,只采用一个while加一个for,思路上是一样的,但注意具体的细节差异
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution :def averageOfLevels (self, root: Optional [TreeNode] ) -> List [float ]:if not root:return []while queue:sum = 0 len (queue)for node in range (cnt):0 )sum += node.valif node.left:if node.right:sum /cnt)return res
时间复杂度 第一个算法
102 二叉树的层序遍历 Medium 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
102.1
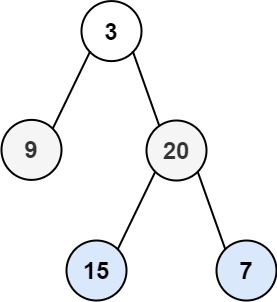
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
思路 和前一题一样,按照题意的顺序遍历即可,只需要去掉计算平均值这个步骤就可以,用前议题已经优化后的思路会比第一种的更快(leetcode上能超越97.73%的人)
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution :def levelOrder (self, root: Optional [TreeNode] ) -> List [List [int ]]:if not root:return []while queue:for i in range (len (queue)):0 )1 ].append(node.val)if node.left:if node.right:return res
时间复杂度 时间复杂度O(n),空间复杂度O(n),执行时间29ms,消耗内存17.1MB
103 二叉树的锯齿形层次遍历 Medium 给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:
103.1
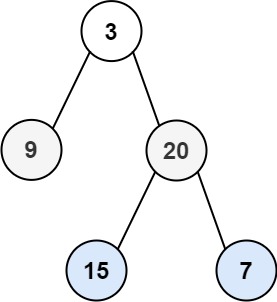
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100
思路 这题和前一道题唯一一个不同就在于对奇偶层的不同操作。当我们在处理这个时一个取余就可与做到,当奇数层时将节点正常进行添加,当偶数层时对节点值进行倒序添加。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution :def zigzagLevelOrder (self, root: Optional [TreeNode] ) -> List [List [int ]]:if not root:return []while queue:for i in range (len (queue)):0 )if len (res) % 2 == 1 :1 ].append(node.val)else :1 ].insert(0 , node.val)if node.left:if node.right:return res
时间复杂度 时间复杂度O(n),空间复杂度O(n),执行时间40ms,消耗内存16.6MB
总结——层次遍历BFS模板 这四道题可以看出基本上都是一套思路,虽然第一题不太一样。
但看其余三道题可以看出都是同一个思路去做,在细微差别上进行部分修改添加条件。
模板如下
二叉树层次遍历(BFS)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution :def traversalTemplate (self, root: Optional [TreeNode] ) -> List [数据类型]:if not root:return []while queue:for i in range (len (queue)):0 )if node.left:if node.right:return res