leetcode刷题记录——分治

108 将有序数组转换为二叉搜索树 Easy

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵

平衡

二叉搜索树。

示例 1：

img

1
2
3
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

img

1
2
3
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 按 严格递增 顺序排列

思路

这里需要回顾下我们之前看过的二叉搜索树的概念，详细请见leetcode刷题记录——二叉搜索树

然后借助我们的概念，root节点就是整个nums的中间位置，然后递归就可以了。

代码

1
2
3
4
5
6
7
8
9
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        if not nums:
            return None
        mid = len(nums) // 2
        root = TreeNode(nums[mid])
        root.left = self.sortedArrayToBST(nums[:mid])
        root.right = self.sortedArrayToBST(nums[mid+1:])
        return root

时间复杂度

时间复杂度O(n)，空间复杂度O(log n)，执行时间43ms，消耗内存17.7MB

148 排序链表 Medium

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：

img

1
2
输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

img

1
2
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

1
2
输入：head = []
输出：[]

提示：

  • 链表中节点的数目在范围 [0, 5 * 104] 内
  • -105 <= Node.val <= 105

思路

首先需要明确的一点是我们需要用到两个方法，一个将链表拆分为两部分，一个用来合并链表

拆分部分需要用到快慢指针，合并部分需要用到虚拟节点和尾节点

其余直接看代码，写了注释

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if not head or not head.next:
            return head
        # 使用快慢指针找到链表中间节点
        slow, fast = head, head.next
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
        # 将链表分为两部分
        second = slow.next
        slow.next = None
        # 递归地对两部分链表进行排序
        left = self.sortList(head)
        right = self.sortList(second)
        # 合并链表
        return self.merge(left, right)
    
    def merge(self, left, right):
        dummy = tail = ListNode(0)
        # 合并有序链表
        while left and right:
            if left.val < right.val:
                tail.next = left
                left = left.next
            else:
                tail.next = right
                right = right.next
            tail = tail.next
        # 剩余节点连接到合并后的尾部
        tail.next = left if left else right
        return dummy.next

时间复杂度

时间复杂度O(nlog n)，空间复杂度O(log n)，执行时间294ms，消耗内存31.4MB

427 建立四叉树 Medium

给你一个 n * n 矩阵 grid ，矩阵由若干 0 和 1 组成。请你用四叉树表示该矩阵 grid 。

你需要返回能表示矩阵 grid 的 四叉树 的根结点。

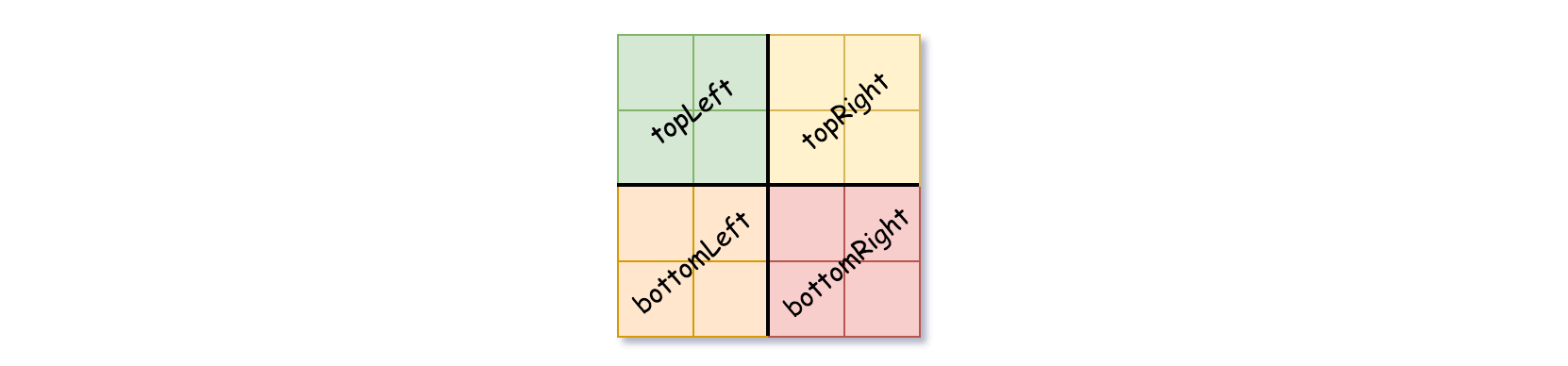
四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

  • val：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False。注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制 接受 。
  • isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False 。
1
2
3
4
5
6
7
8
class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

我们可以按以下步骤为二维区域构建四叉树：

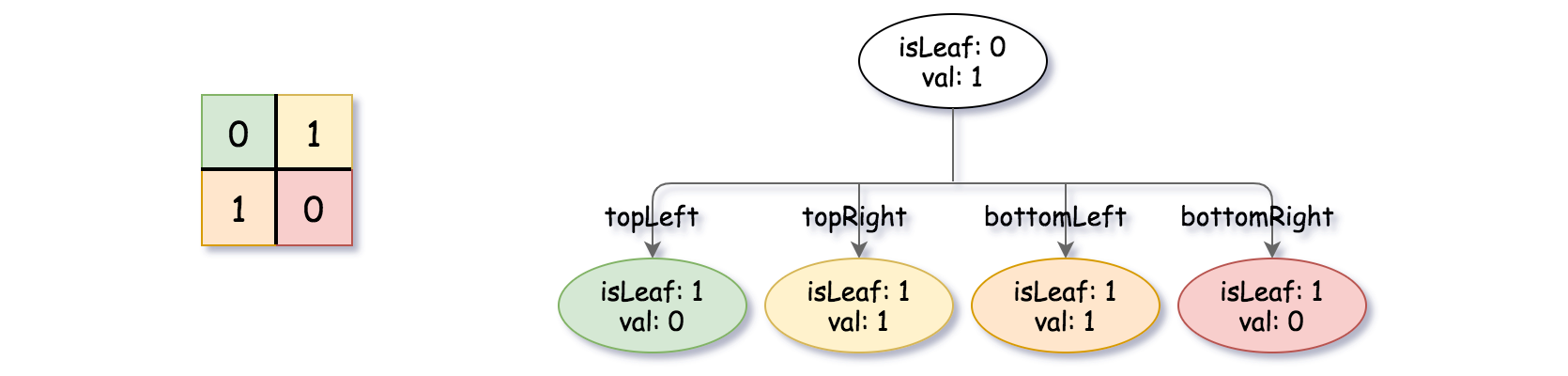
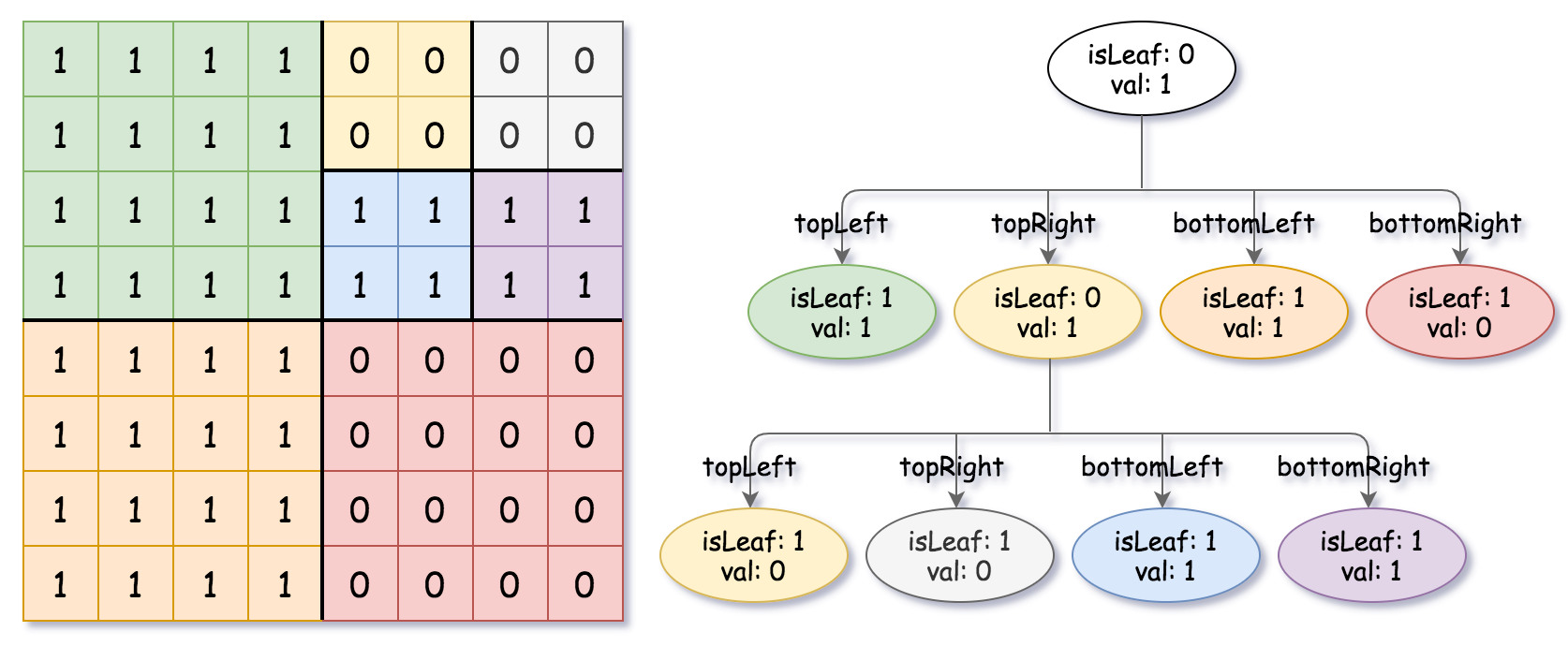
  1. 如果当前网格的值相同（即，全为 0 或者全为 1），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
  2. 如果当前网格的值不同，将 isLeaf 设为 False， 将 val 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
  3. 使用适当的子网格递归每个子节点。

img

如果你想了解更多关于四叉树的内容，可以参考 wiki 。

四叉树格式：

你不需要阅读本节来解决这个问题。只有当你想了解输出格式时才会这样做。输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。

它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。

如果 isLeaf 或者 val 的值为 True ，则表示它在列表 [isLeaf, val] 中的值为 1 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 0 。

示例 1：

img

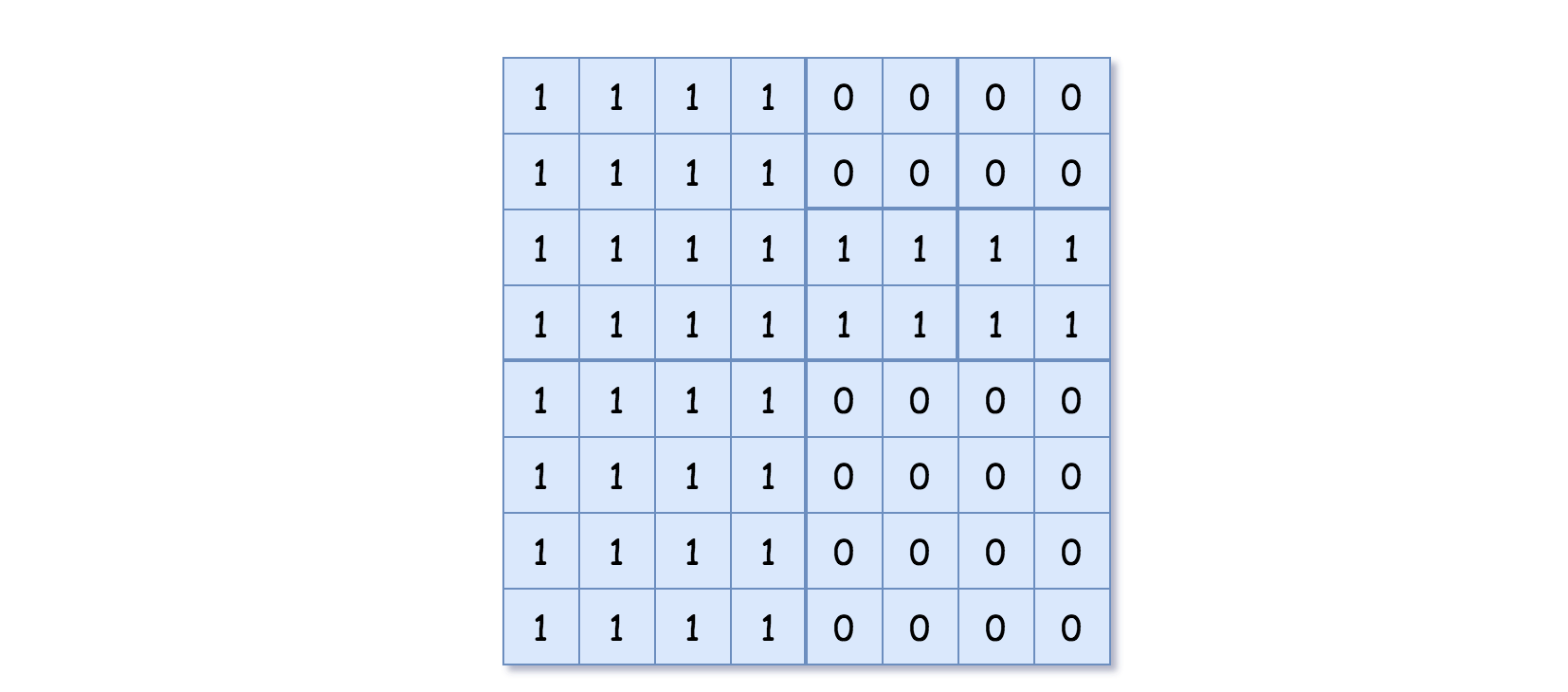
1
2
3
4
输入：grid = [[0,1],[1,0]]
输出：[[0,1],[1,0],[1,1],[1,1],[1,0]]
解释：此示例的解释如下：
请注意，在下面四叉树的图示中，0 表示 false，1 表示 True 。

img

示例 2：

img

1
2
3
4
5
6
输入：grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
输出：[[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
解释：网格中的所有值都不相同。我们将网格划分为四个子网格。
topLeft，bottomLeft 和 bottomRight 均具有相同的值。
topRight 具有不同的值，因此我们将其再分为 4 个子网格，这样每个子网格都具有相同的值。
解释如下图所示：

img

提示：

  1. n == grid.length == grid[i].length
  2. n == 2x 其中 0 <= x <= 6

思路

主要用到两个函数，same和dfs。same函数用于检查二维数组中所有元素是否相同，dfs函数用于递归构建四叉树，所用到的四个参数主要用于处理当前矩阵区域的起始行结束行起始列结束列。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def construct(self, grid: List[List[int]]) -> 'Node':
        # 辅助函数：检查从 (a, c) 到 (b, d) 的矩形区域内的所有元素是否相同
        def same(a, b, c, d):
            cur = grid[a][c]  # 获取区域左上角的值
            for i in range(a, b):
                for j in range(c, d):
                    if grid[i][j] != cur:  # 如果发现不同值，返回 False
                        return False
            return True  # 区域内所有元素相同，返回 True
        
        # 深度优先搜索函数：递归构建四叉树
        def dfs(rs, re, ls, le):
            if same(rs, re, ls, le):  # 如果当前区域内的所有元素相同
                node = Node(grid[rs][ls], True, None, None, None, None)  # 创建叶子节点
            else:
                node = Node(grid[rs][ls], False, None, None, None, None)  # 创建非叶子节点
                row_middle = (rs + re) // 2  # 计算中间行索引
                col_middle = (ls + le) // 2  # 计算中间列索引
                # 递归构建四个子节点
                node.topLeft = dfs(rs, row_middle, ls, col_middle)
                node.topRight = dfs(rs, row_middle, col_middle, le)
                node.bottomLeft = dfs(row_middle, re, ls, col_middle)
                node.bottomRight = dfs(row_middle, re, col_middle, le)
            return node  # 返回当前构建的节点
        
        l = len(grid)  # 获取输入二维数组的长度
        return dfs(0, l, 0, l)  # 从整个矩阵的左上角到右下角开始递归构建四叉树

时间复杂度

时间复杂度$O(n^2logn)$，空间复杂度$O(logn)$，执行时间89ms，消耗内存17.35MB

23 合并 K 个升序链表 Hard

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

1
2
3
4
5
6
7
8
9
10
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

1
2
输入：lists = []
输出：[]

示例 3：

1
2
输入：lists = [[]]
输出：[]

提示：

  • k == lists.length
  • 0 <= k <= 10^4
  • 0 <= lists[i].length <= 500
  • -10^4 <= lists[i][j] <= 10^4
  • lists[i] 按 升序 排列
  • lists[i].length 的总和不超过 10^4

思路

整体思路上借助最小堆的特性来做，堆中的元素需要包含节点的值，节点的唯一标识，节点本身

关于最小堆的特性：

  • 最小堆是一种完全二叉树，这意味着除了最后一层外，其他层都是满的，并且最后一层的节点都尽量靠左排列。
  • 对于任意节点 i，其左子节点 2*i + 1 和右子节点 2*i + 2 的值都大于或等于节点 i 的值。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        dummy = ListNode(0)
        p = dummy
        pq = []
        
        # 将每个链表的头节点压入堆中
        for head in lists:
            if head:
                heapq.heappush(pq, (head.val, id(head), head))
        
        # 当堆不为空时，执行以下操作
        while pq:
            # 从堆中弹出值最小的节点
            node = heapq.heappop(pq)[2]
            p.next = node
            
            # 如果该节点有下一个节点，则将下一个节点压入堆中
            if node.next:
                heapq.heappush(pq, (node.next.val, id(node.next), node.next))
            
            p = p.next
        
        return dummy.next

时间复杂度

时间复杂度$O(nlogk)$，空间复杂度O(n + k)，执行时间49ms，消耗内存18.8MB

刷题记录
#Leetcode #刷题 #分治
leetcode刷题记录——分治
https://www.lx02918.ltd/2024/09/03/leetcode-分治/
作者
Seth
发布于
2024年9月3日
许可协议