陌陌笔试——推荐算法-计算智能算法笔试

前言

说实话，陌陌这次的笔试真的真的让人感觉到了原来我真的会点东西啊，废话不多说，直接上题目。

对了，前提需要说一下，代码为核心代码模式，且需要将结果设为result，最终函数返回1，后续会人工判卷（有一说一我自己是觉得人工判卷相对来说会比系统自动要好一些，最起码有主观看法）。

寻找支配点

P为给定的二维平面整数点集。定义P中某点x，如果x满足P中任意点都不在x的右上方区域内（横纵坐标都大于x），则称其为一个支配点。

如下图所示，蓝色点位该点集中的支配点集合

寻找支配点

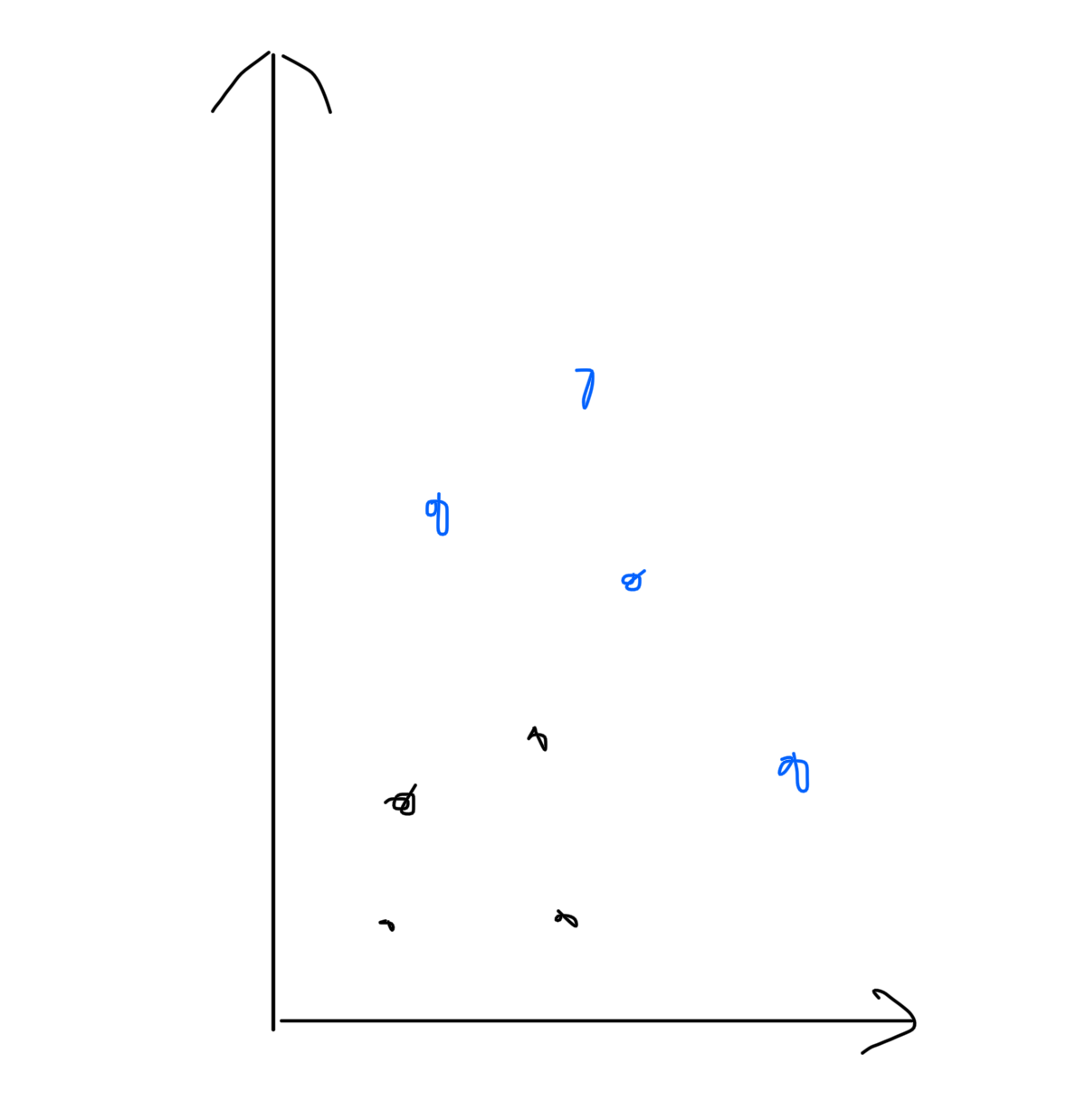
请实现代码，找到给定的人以及和P中的所有支配点并输出。（所有点的横纵坐标不重复）

输入：二维数组，表示点集P

输出：二维数组，n个支配点的点集Q

示例：

输入 P=[[1, 2], [5, 3], [4, 6], [7, 5], [9, 0]]

输出 [[4, 6], [7, 5], [9, 0]]

代码

from typing import List
class Solution:
    def main(self , P: List[List[int]]) -> int:
        P.sort(key = lambda p: (-p[0], p[1]))
        result = []
        max_y = 1
        for x, y in P:
            if y > max_y:
                result.append([x, y])
        self.result = result
        return 1

非极大值抑制

非极大值抑制（Non-Maximum Suppression，NMS）是一种用于目标检测的算法，旨在从多个重叠的候选框中选择出最优的框。其基本思想是抑制那些不是局部最大值的元素，从而减少冗余的检测结果。

NMS的工作原理

1. 局部最大搜索：NMS算法通过对候选框的得分进行排序，选择得分最高的框作为参考框。
2. 计算重叠度：对于其他候选框，计算它们与当前参考框的重叠度（交并比，IoU）。如果某个候选框的IoU大于设定的阈值（通常在0.3到0.5之间），则认为它与参考框指向同一目标，因而将其剔除。
3. 重复过程：从剩余的候选框中再次选择得分最高的框，重复上述步骤，直到没有候选框可以被剔除为止。

NMS在计算机视觉领域的应用非常广泛，包括视频目标跟踪、数据挖掘、3D重建和目标识别等

(以上资料来源于网络)

输入：

boxes为二维数组，其中每个元素是一维数组[x1, y1, x2, y2]，分别表示框的左上角和右下角坐标。scores是一个一维数组，每个元素表示每个框的置信度。两个的元素个数是相互对应的，iou_threshold表示用于移除重叠框的交并比阈值。

输出：

一个一维数组，表示所有留下框在原始列表中的下表，按照从小到大排序。

提示：

框面积计算公式为（y2 - y1) * (x2 - x1)

交并比的计算公式为：两框的交集面积除以并集面积

示例：

输入：

boxes = [[x11, y11, x21, y21], [x12, y12, x22, y22], [x13, y13, x23, y23]], scores = [0.75, 0.7, 0.8], iou_threshold = 0.7

输出：

[0, 2]

class Solution:
    def main(self, boxes: List[List[int]], sorces: List[float], iou_threshold: float) -> int:
        def calculate_iou(box1, box2):
            x1 = max(box1[0], box2[0])
            y1 = max(box1[1], box2[1])
            x2 = min(box1[2], box2[2])
            y2 = min(box1[3], box2[3])
            
            intersection = max(0, x2 - x1) * max(0, y2 - y1)
            area1 = (box1[2] - box1[0]) * (box1[3] - box1[1])
            area2 = (box2[2] - box2[0]) * (box2[3] - box2[1])
            union = area1 + area2 - intersection
            
            return intersection / union if union > 0 else 0
        n = len(boxes)
        indices = list(range(n))
        indices.sort(key = lambda i: sorces[i], reverse = True)
        
        result = []
        while indices:
            idx = indices[0]
            result.append(idx)
            indices = indices[1:]
            
            indices = [i for i in indices if calculate_iou(boxes[idx], boxes[0]) <= iou_threshold]
            
            result.sort()
            result = result
            return 1

序列置换

给一个长度为N（N<1000）的正整数序列（1~N），我们称之为A。将上述序列随机重新排列后的序列称之为B序列。使用B序列作为一个置换，来对A序列进行操作。置换是指将A序列中的第B[i]个元素，挪到第i个位置。请实现一个函数，输入将A序列置换K次之后的序列。注意K可能会非常大($K < 10^8$)

输入：A序列、B序列以及K

输出：置换后序列

示例：

输入：

A = [1, 2, 3], B = [3, 1, 2], k = 2

输出：[2, 3, 1]

说明：

A序列经过B序列置换后变为312，再经过231

Q1：请简述算法思路和时间空间复杂度

Q2：编程实现

class Solution:
    def main(self, A: List[int], B: List[int], k: int) -> int:
        n = len(A)
        result = [0] * n
        visited = [False] * n
        
        for i in range(n):
            if not visited[i]:
                cycle = []
                j = i
                while not visited[j]:
                    visited[j] = True
                    cycle.append(j)
                    j = B[j] - 1
                cycle_length = len(cycle)
                for m in range(cycle_length):
                    result[cycle[(m + K) % cycle_length]] = A[cycle[m]]
        return 1

思路

1. 构建循环：遍历A的每个元素，使用i作为索引如果没有被访问则从这里开始，沿着B数组定义的置换元素构建一个置换循环。使用cycle记录循环中给所有元素的索引
2. 处理置换循环：遍历cycle，记长度为cycle_length，对每个元素都置换到新位置，位置是计算得出的

时间复杂度

时间复杂度O(n)，空间复杂度O(n)

后记

这次的题相对来说其实属于easy和medium范畴了。但是由于没有设定结果所以也没办法看自己最终能够通过多少，不过我的思路应该是大差不差的，如果有什么问题还请大家在评论里指出，啾咪💞