西山居笔试——游戏AI算法A卷

柱状图中最大矩形

对应leetcode84，属于hard

这里需要说明一下这道题第一反应会和最大容器和接雨水有点像，会考虑到双指针，但是题目实际上用到的是单调栈和哨兵

原题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

考试题目

给定一个数组heights, 长度为n, height[i]是第i根的高度, 那么height[i]表示的直方图, 能够形成的最大矩形是多少?

1.每个直方图底座宽度为1
2.直方图都是相邻的
3.如果不能形成矩形, 返回0即可
4.保证返回的结果不会超过2³¹-1

数据范围:
0<=heights[i]<=10 ^4
0<=heights.length<=10 ^5

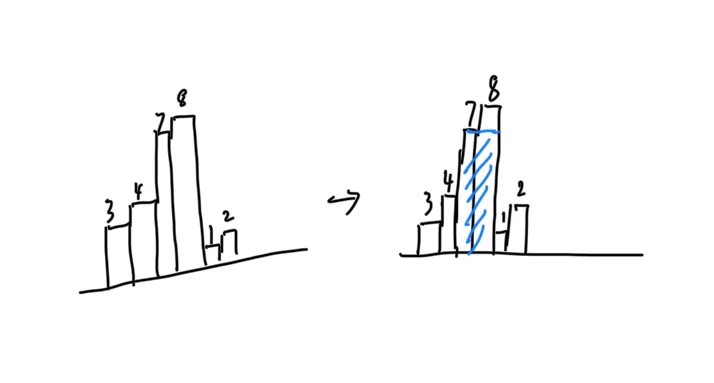
如输入[3,4,7,8,1,2], 那么如下:

84.1

输入：

heights = [3, 4, 7, 8, 1, 2]

输出

14

思路

1. 单调栈：使用单调栈来存储柱子的索引，并保持栈中的柱子高度是递增的
2. 哨兵：在原始高度数组的前后都添加一个高度为0的柱子，这样可以简化边界处理
3. 遍历过程
   1. 当栈不为空且当前柱子的高度小于栈顶柱子的高度时能够找到一个可以计算面积的矩形
   2. 弹出栈顶，计算以该柱子高度为高的最大矩形面积
   3. 如果栈为空，宽度就是当前索引i；否则宽度时当前索引i减去新的栈顶索引再减1
   4. 更新最大面积
   5. 将当前柱子的索引入栈
4. 结果：遍历结束后在max_area中存储就是最大面积

总的来说核心思想就是对每个柱子都左右扩展，直到遇到比它矮的柱子，这样就找到了以这个柱子高度为高的最大矩形

代码

class Solution:
    def largestRectangleArea(self , heights: List[int]) -> int:
        stack = []
        heights = [0] + heights + [0]
        max_area = 0
        for i in range(len(heights)):
            while stack and heights[stack[-1]] > heights[i]:
                h = heights[stack.pop()]
                w = i if not stack else i - stack[-1] - 1
                max_area = max(max_area, h * w)
            stack.append(i)
        return max_area

时间复杂度

时间复杂度为O(n)，空间复杂度为O(n)

压缩字符串Ⅱ

这道题对应的是leetcode1531，属于hard。这道题需要事先说明我只通过了26.73%，思路上应该没啥问题，但是过不去是为什么我还在看原因。

原题目

行程长度编码 是一种常用的字符串压缩方法，它将连续的相同字符（重复 2 次或更多次）替换为字符和表示字符计数的数字（行程长度）。例如，用此方法压缩字符串 "aabccc" ，将 "aa" 替换为 "a2" ，"ccc" 替换为 “c3”。因此压缩后的字符串变为“a2bc3”` 。

注意，本问题中，压缩时没有在单个字符后附加计数 '1' 。

给你一个字符串 s 和一个整数 k 。你需要从字符串 s 中删除最多 k 个字符，以使 s 的行程长度编码长度最小。

请你返回删除最多 k 个字符后，s 行程长度编码的最小长度 。

示例 1：

输入：s = "aaabcccd", k = 2
输出：4
解释：在不删除任何内容的情况下，压缩后的字符串是 "a3bc3d" ，长度为 6 。最优的方案是删除 'b' 和 'd'，这样一来，压缩后的字符串为 "a3c3" ，长度是 4 。

示例 2：

输入：s = "aabbaa", k = 2
输出：2
解释：如果删去两个 'b' 字符，那么压缩后的字符串是长度为 2 的 "a4" 。

示例 3：

输入：s = "aaaaaaaaaaa", k = 0
输出：3
解释：由于 k 等于 0 ，不能删去任何字符。压缩后的字符串是 "a11" ，长度为 3 。

提示：

• 1 <= s.length <= 100
• 0 <= k <= s.length
• s 仅包含小写英文字母

考试题目

利用字符串重复出现的次数，编写一种方法，最多可以先删除K个字符，再实现字符串压缩，返回压缩后的字符串的最小长度。比如，字符串aabccccaaa，k=0时，会压缩为a2bc5a3，返回7。

例
1.如果只有一个字符，1不用写
2.新增一个先删除k个字符的处理，也可以不删除，也可以删除少于k个字符，要达到压缩后字符串的长度为最小
3.字符串中只包含小写英文字母（a至z）

数据范围：
0<=字符串长度<=100
0<=k<=字符串长度

示例1

输入
“aabccccaaa”,0

输出
7

说明
压缩后的字符串为”a2bc5a3”，长度为7

思路

1. 递归函数：
   • 内部定义的 compress 函数用于递归地计算字符串从索引 idx 开始压缩的最小结果，同时追踪已删除的字符数量 deleted。
2. 终止条件：
   • 当 idx 达到字符串长度 n 时，表示已经处理完所有字符，返回 0。
3. 备忘录：
   • 使用字典 memo 来存储中间结果，以避免重复计算。
4. 删除选项：
   • 如果已经删除的字符数小于 k，则可以选择删除当前字符，这个选项的结果为 compress(idx + 1, deleted + 1)。
5. 保留选项：
   • 保留当前字符，然后计算与后续相同字符的数量。如果存在连续相同的字符，则需要计算这些字符的数量并进行压缩。
   • keep_option 开始时为 1（表示至少保留当前字符），并根据连续相同字符的数量来更新。
6. 选择最优解：
   • 最终，比较删除选项和保留选项的结果，选择其中的最小值，并将结果存储到 memo 中。
7. 返回结果：
   • 最后，调用 compress 函数从索引 0 和已删除字符数 0 开始，最终返回字符串的压缩结果。

代码

class Solution:
    def compressString(self , s: str, k: int) -> int:
        n = len(s)
        memo = {}
        def compress(idx, deleted):
            if idx == n:
                return 0
            if (idx, deleted) in memo:
                return memo[(idx, deleted)]
            
            deleted_option = float('inf')
            if deleted < k:
                deleted_option = compress(idx + 1, deleted + 1)
            keep_option = 1
            count = 1
            for j in range(idx + 1, n):
                if s[j] == s[idx]:
                    count += 1
                else:
                    break
            if count > 1:
                keep_option += len(str(count))
            keep_option += compress(idx + count, deleted)
            result = min(deleted_option, keep_option)
            memo[(idx, deleted)] = result
            return result
        
        return compress(0, 0)

leetcode官方答案代码

class Solution:
    def getLengthOfOptimalCompression(self, s: str, k: int) -> int:
        calc = lambda x: 1 if x == 1 else (2 if x < 10 else (3 if x < 100 else 4))

        n = len(s)
        f = [[10**9] * (k + 1) for _ in range(n + 1)]
        f[0][0] = 0
        
        for i in range(1, n + 1):
            for j in range(min(k, i) + 1):
                if j > 0:
                    f[i][j] = f[i - 1][j - 1]
                same = diff = 0
                for i0 in range(i, 0, -1):
                    if s[i0 - 1] == s[i - 1]:
                        same += 1
                        f[i][j] = min(f[i][j], f[i0 - 1][j - diff] + calc(same))
                    else:
                        diff += 1
                        if diff > j:
                            break
        return f[n][k]

作者：力扣官方题解
链接：https://leetcode.cn/problems/string-compression-ii/solutions/379042/ya-suo-zi-fu-chuan-ii-by-leetcode-solution/
来源：力扣（LeetCode）

我写的时候第一遍直接写的dp，过了15还是16，代码贴一下吧，给大家个错误展示

class Solution:
    def compressString(self , s: str, k: int) -> int:
        n = len(s)
        dp = [[float('inf') * (k + 1) for _ in range(n + 1)]]
        dp[0][0] = 0
        for i in range(1, n + 1):
            for j in range(0, k + 1):
                if dp[i - 1][j] < float('inf'):
                    if j + 1 <= k:
                        dp[i][j + 1] = min(dp[i][j + 1], dp[i - 1][j])
                    cnt = 0
                    for m in range(i, n + 1):
                        if s[m - 1] == s[i - 1]:
                            cnt += 1
                            cost = 1
                            if cnt >= 100:
                                cost += 3
                            elif cnt >= 10:
                                cost += 2
                            elif cnt >= 2:
                                cost += 1
                            if j + (m - i) <= k:
                                dp[m][j + (m - i)] = min(dp[m][j + (m - i)], dp[i - 1][j] + cost)
                        else:
                            continue
        return min(dp[n])

时间复杂度

时间复杂度O(n * k)，空间复杂度O(n * k)

编程两道题就说到这里，如果有同学第二题写出来的一定一定要评论一下，讲讲思路。这题我考场上是真没搞明白😭